The perceptron algorithm is a key algorithm to understand when learning about neural networks and deep learning. This post will show you how the perceptron algorithm works when it has a single layer and walk you through a worked example.
What the perceptron algorithm does
The perceptron is a binary classifier that linearly separates datasets that are linearly separable [1].
So, if we have a dataset such as this:
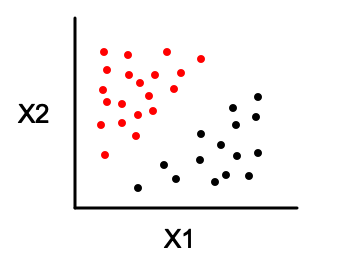
The perceptron algorithm will find a line that separates the dataset like this:
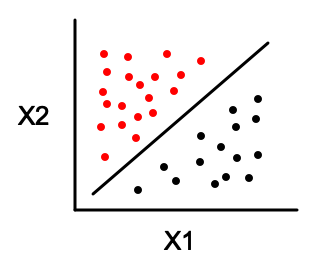
Note that the algorithm can work with more than two feature variables. Also, there could be infinitely many hyperplanes that separate the dataset, the algorithm is guaranteed to find one of them if the dataset is linearly separable. Furthermore, if the data is not linearly separable, the algorithm does not converge to a solution and it fails completely [2].
How the perceptron algorithm works
To start here are some terms that will be used when describing the algorithm. Their meanings will become clearer in a moment.

Note that a feature is a measure that you are using to predict the output with. If you are trying to predict if a house will be sold based on its price and location then the price and location would be two features.
Below is how the algorithm works. For this example, we’ll assume we have two features.
- Assign a weight to each feature. In this case, there are two features so we have two weights. Set the initial values of the weights to 0.
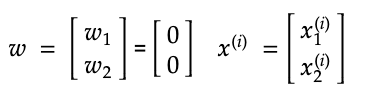
2. For the first training example, take the sum of each feature value multiplied by its weight then add a bias term b which is also initially set to 0.
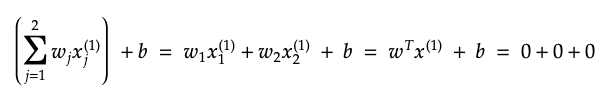
Note that this represents an equation of a line. Currently, the line has 0 slope because we initialized the weights as 0. We will be updating the weights momentarily and this will result in the slope of the line converging to a value that separates the data linearly.
3. Apply a step function and assign the result as the output prediction.
Note that, later, when learning about the multilayer perceptron, a different activation function will be used such as the sigmoid, RELU or Tanh function.
4. Update the values of the weights and the bias term.
Note that if yhat = y then the weights and the bias will stay the same.
5. Repeat steps 2,3 and 4 for each training example.
6. Repeat until a specified number of iterations have not resulted in the weights changing or until the MSE (mean squared error) or MAE (mean absolute error) is lower than a specified value.
7. Use the weights and bias to predict the output value of new observed values of x.
Below is a visual representation of a perceptron with a single output and one layer as described above.
Worked example
Below is a worked example.



Useful resources
Below are some resources that are useful.
Hands on Machine Learning 2 – Talks about single layer and multilayer perceptrons at the start of the deep learning section.
